CogniFit - Probability estimation of being involved in a motor vehicle crash as a function of sociodemographic and cognitive data.

Disclaimer: All material presented in this brief data analysis report, unless specifically indicated otherwise, is under current development by a group of external independent researchers. The analysis presented in this report is provided for information purposes only and are not to be used or considered as a peer-reviewed scientific publication.

Original name: Probability estimation of being involved in a motor vehicle crash as a function of sociodemographic and cognitive data.

Authors: Jon Andoni Duñabeitia ^{1, 2}, José Luis Tapia ¹.

• 1. Centro de Ciencia Cognitiva - C3 (Center for Cognitive Sciences), Universidad Nebrija (Madrid, Spain).
• 2. AcqVA Aurora Center, The Artic University of Norway (Tromsø, Norway).

Main conclusions:

There is a robust relationship between CogniFit's "Estimation" cognitive score and various types of traffic accidents, independent of the gender of the drivers (all coefficients are greater than 0.75). Age, gender, and the drivers' Estimation score are good predictors of the group probability of being involved in a fatal car accident (accounting for 98.3% of the variance, R = 0.966, R2 = 0.983), of being involved in an accident with injuries (explaining 96.2% of the variance, R = 0.981, R2 = 0.962), and of being involved in accidents with material damage (explaining 95.8% of the variance, R = 0.979, R2 = 0.958).

CogniFit® measures

Data were collected from two independently conducted cognitive tasks measuring participants’ estimation skills using smartphones as well as personal computers. A total of 20,231 persons from 123 different countries and ages between 18 and 78 years old completed these two CogniFit® tasks (10,627 females, 9,606 males).

One of the tasks measured participants’ ability to estimate the duration of a continuous auditory stimulus by asking them to interrupt an ongoing auditory stimulus so as to reproduce the exact length of time of a previously presented continuous auditory stimulus. The other task measured participants’ ability to estimate the speed of moving objects, the distance covered and to be covered, and how the interaction of speed and distance affects the movement of an object. The dependent variables obtained in these two tasks correspond to the overall percentage of accuracy of each participant, with better participant precision indicated by a higher percentage score. From these variables, a composite CogniFit® measure of each person’s estimation abilities was computed.

Motor vehicle crash measures

The data were obtained from the National Highway Traffic Safety Administration (NHTSA) of the United States via the Fatality and Injury Reporting System Tool (FIRST). All the data from 2014 through 2018 corresponding to the net number of persons involved in three types of motor vehicle accidents were collected from the public data querying and reporting service, filtered by the age of the driver (persons from 18 to 78 years old were selected)

First, data were collected corresponding to drivers involved in crashes involving human fatalities from the Fatality Analysis Reporting System (FARS), 2004-2017, and the Annual Report File (ARF), 2018.

Second, data from drivers involved in injury-only motor vehicle accidents were obtained from the National Automotive Sampling System General Estimates System (NASS-GES), 2004-2015, and the Crash Report Sampling System (CRSS), 2016-2017.

And third, data corresponding to the drivers involved in property-damage-only motor vehicle crashes were collected from the same sources.

Starting assumptions

Age is a critical factor both for the frequency of crashes of each type and the severity (with older drivers being involved in fewer crashes). In addition, age is also a significant moderator of the estimation abilities (the results of the CogniFit® composite demonstrate lower scores for older persons).

With these two assumptions in mind, the correlation analysis should show a significant direct relationship between the number of accidents and the results in the CogniFit® estimation tasks, given that age could be driving these observations. But more importantly, if the CogniFit® composite scores represent an additional benefit for the estimation of any type of motor vehicle accident, this should be shown in a regression analysis once the effect of age has been accounted for.

Nonetheless, it should be kept in mind that the two data sources correspond to different samples from different populations. The motor vehicle crash measures were obtained from the National Highway Traffic Safety Administration (NHTSA) of the United States, thus mainly if not exclusively involving American citizens. In contrast, the CogniFit® measures were obtained from a diverse sample from different origins (123 countries). Hence, caution is advised when considering the results of the following analysis given the potential existence of Type I error as a consequence of a hidden impact of spurious correlations.

However, several notes should be made at this regard. First, it is worth considering that the results of a given cognitive test with an ample and representative sample size and adequate psychometric properties such as CogniFit®’s (see this link for details on the validity and reliability of the assessment tools) could be taken as normative data and consequently applied to other similar samples by means of generalization. And second, and conditional upon the premise of having sufficiently large sample sizes that could allow for generalizability and transferability, it should be considered that using parameter estimates resulting from either a normative dataset or an analysis to account for variance from a different sample is an increasingly popular means of extrapolation (see, for instance, this article). This is especially relevant in the context of the current analysis, considering that getting national data on motor vehicle crashes of a cohort who has been assessed with a cognitive battery immediately before they were involved in the accidents is virtually impossible. In any case, and in an attempt to orient the analysis towards samples with a similar background, a parallel approach was carried out considering only the data of the individuals that had completed the CogniFit® assessment and who indicated that were US citizens. This sub-selection included 1290 females and 762 males. Importantly, when the same correlation analysis presented immediately below was run on this American sample, parallel effects were obtained, reinforcing the main conclusions (with Pearson’s r>.55 and Spearman’s rho>.40 for the analysis of male data, and Pearson’s r>.57 and Spearman’s rho>.42 for the female data; all ps<.001).

Correlation analysis

The averaged CogniFit® and NHTSA data for males and females with ages between 18 and 78 years old were statistically analyzed following a correlational approach based on Spearman’s rank coefficient for monotonic functions and Pearson’s correlation coefficient for linear relationships among variables.

The mean percentages of accuracy for both males and females in the two CogniFit® tasks were correlated with the raw data from male and female drivers involved in 1) fatal crashes, 2) injury-only crashes, and 3) property-damage-only crashes.

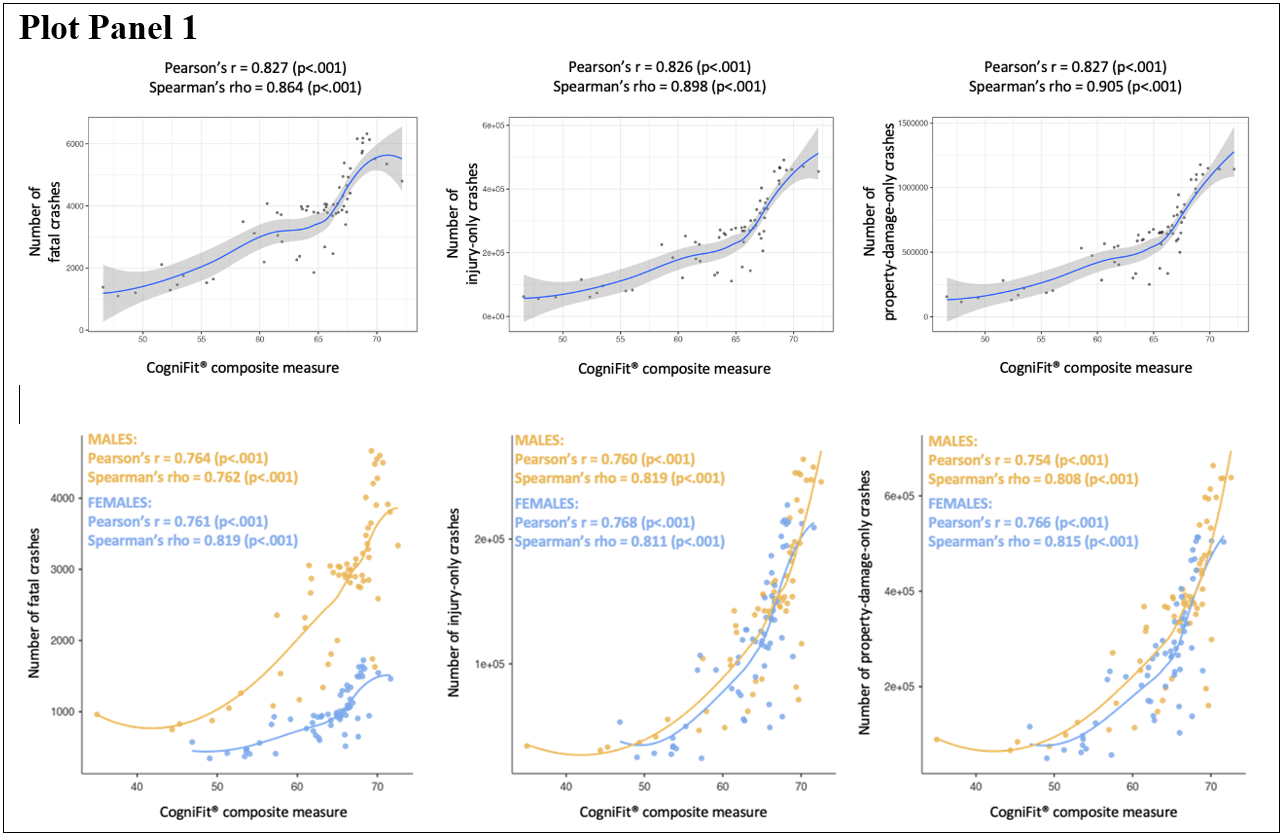
The results showed strong positive correlations between the composite CogniFit® measures and the number of the three types of crashes across ages, with correlation coefficients higher than 0.80 in all cases. The following graphs represent these relationships among the variables together with the corresponding correlation coefficients. Each point represents the value at each specific age point, and the blue line corresponds to the fitted LOESS line (see Plot Panel 1).

In addition, a similar procedure was followed splitting the data according to the drivers’ gender (male or female). Correlation coefficients were highly similar for both gender groups, demonstrating the robustness of the intrinsic relationship between the CogniFit® composite measure and the types of crashes, independently of the gender of the drivers (with all coefficients higher than 0.75). The corresponding graphs display this relationship with each gender group represented in a different color (see Plot Panel 1).

Regression analysis

A linear regression analysis was carried out using the data of the different types of crashes converted to the percentage of crashes per type and gender from the total as dependent measures, and the age of the drivers, their gender, and their CogniFit® composite score as predictive factors, with the interaction between the last two factors also added to the models.

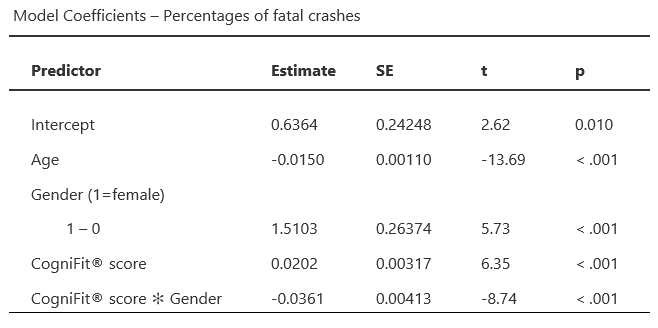
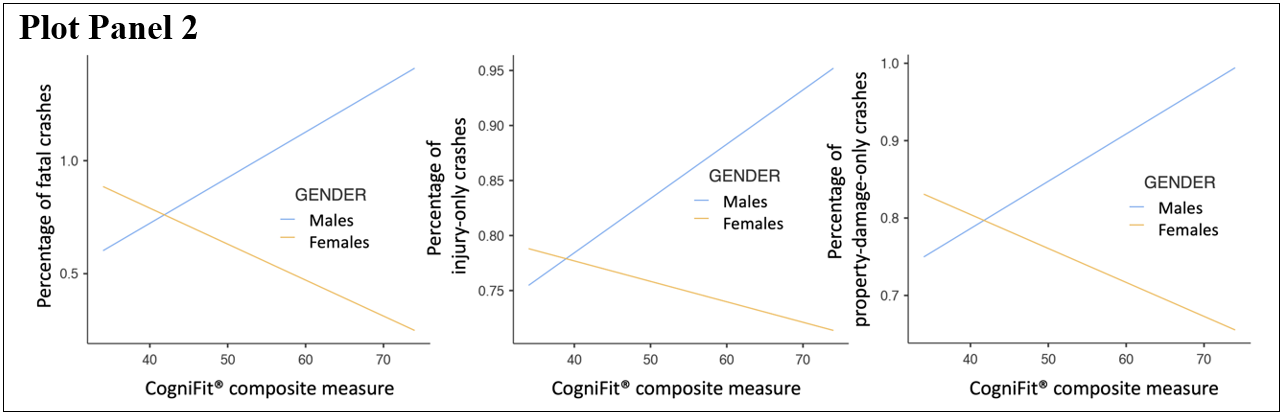
The results corresponding to fatal crashes showed very high goodness-of-fit of the model, explaining 98.3% of the variance as a function of the parameter estimates (R=0.966, R2=0.983). The model coefficients for the different factors showed significant predictive power of age and gender, demonstrating that older drivers were involved in fewer fatal crashes than younger drivers and that women had fewer fatal crashes than men. The CogniFit® composite score also showed a significant effect, suggesting a direct relationship between a person’s estimation skills and the number of fatal crashes. Importantly, this final observation was qualified by a significant interaction between the CogniFit® composite score and the gender. As shown in the graphs (see Plot Panel 2), the influence of the CogniFit® composite scores was different for each gender: For males, higher scores on the CogniFit® composite was associated with a higher risk of being involved in fatal crashes, while for females, higher CogniFit® composite scores were associated with lower percentages of fatal crashes.

Parallel findings were observed for the analysis of the data corresponding to the injury-only motor vehicle crashes. The same model explained 96.2% of the variance (R=0.981, R2=0.962), and the effect of age was significant, as was also the case for the effect of the CogniFit® composite score. Gender and the CogniFit® composite score showed a significant interaction: While males followed the expected direct pattern between the CogniFit® composite score and the number of injury-only crashes, females showed an inverse relationship: for females, higher CogniFit® composite scores were associated with fewer crashes.

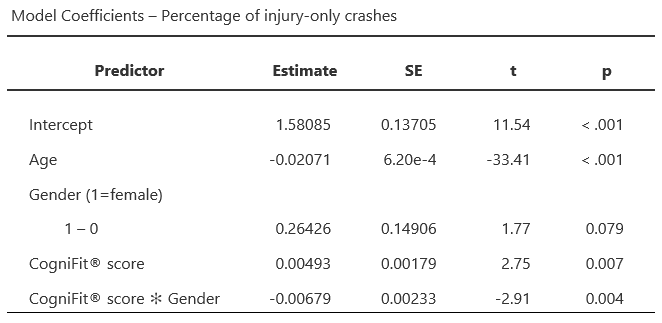
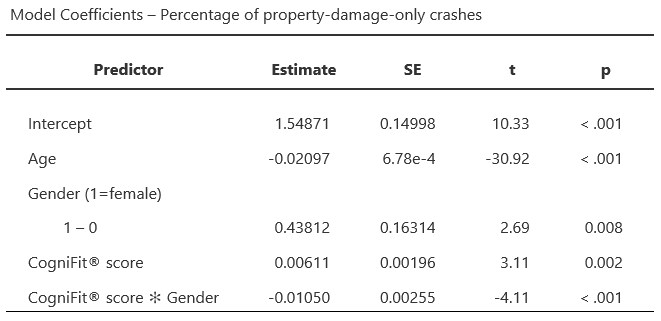
Finally, an analysis of the data corresponding to the property-damage-only motor vehicle crashes was carried out. The same model explained 95.8% of the variance (R=0.979, R2=0.958), and the effects of age, gender, and the CogniFit® composite score were significant. Gender and the CogniFit® composite score showed a significant interaction, once more showing an inverse relationship between the CogniFit® composite scores and the number of injury-only motor vehicle crashes only for female drivers.

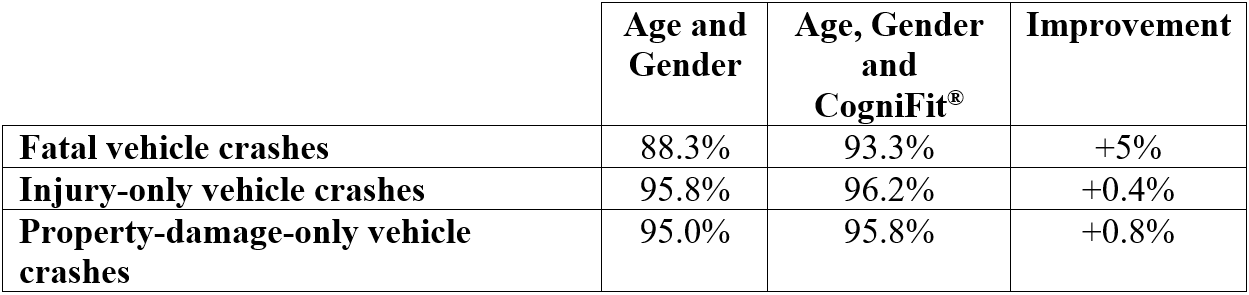
The following table summarizes the explanatory power of the statistical model adding the CogniFit® composite scores vs. a simpler model that only includes the age of the drivers and their gender. As is apparent, in all cases the resulting models are significantly better (as attested by the corresponding statistical model contrasts).